Poker Quiz #2: Base Rates and Combinations

The use of base rates comes up often in poker, and can be useful when making decisions to fold, call, or raise. Most poker games involve hidden cards, but this does not mean we have to blindly guess what these cards might be. By using knowledge of the distribution of random poker hands, we can build an informed estimate of opponents’ possible holdings, even before the hand begins.

To solve for the probability of holding a particular type of hand, we can count all qualifying hand combinations, and divide by all possible combinations. To do this we could manually count all combinations, or we can make use of the formula:

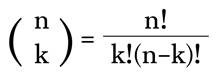
Where n is the total number of cards you are selecting from, and k is the number of cards in a hand.

For example, if you would like to know the probability of being dealt Ace-King of the same suit out of a 52 card deck, you would do the following calculation:

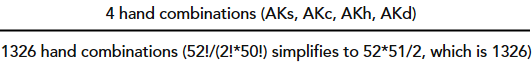
Suppose you are playing a game of 7 card stud. You are one spot off the bring and are dealt (8h,6d) 8s. Everyone folds to you and it is your action versus the bring, who has the 3d showing. Without using knowledge of the folded upcards, your opponent’s hand is a random distribution of the remaining 48 unknown cards in the deck.

What is the probability your opponent has rolled up threes (both hidden cards are threes)?

What is the probability your opponent has a hidden pair higher than your eights?

Now suppose you had paid attention to folded upcards. You saw that the 7h, 7s, 6c, 8d, Td, 4c, and 6s are folded. What is the probability your opponent has a hidden pair higher than your eights? You can assume your opponents’ folds do not give you any additional information on which hidden cards are more likely to be dead.

Now that we know how to estimate base rate holdings, we can extend our analysis to further narrow down our opponents’ ranges. Once an opponent takes an action in a hand, we can immediately start to eliminate hand combinations from our calculation. For example, if an opponent raises you on third street, and you know this particular opponent only plays pairs, the denominator of possible holdings becomes the set of all paired hands. As the hand progresses and you gain more information from the actions on each street, you can continue to narrow your estimate. By the end of the hand, you might find you are left with only a couple of possibilities!