
Before we get into fantasy football strategies, let’s first discuss nontransitivity in preferences. Most of our day-to-day experience is with coherent preferences; if I like Kit Kats more than Mounds, and I like Reese’s Peanut Butter Cups more than Kit Kats, then I must like the PB Cups more than Mounds. (This is the correct ordering of preferences for these candy bars, by the way.) There are times, however, that we can prefer A to B, and B to C, but prefer C to A.
As an example, imagine that you have three dice: Die A has sides [4, 4, 4, 4, 4, 4], Die B has sides [6, 6, 6, 6, 0, 0], and Die C has sides [10, 10, 1, 1, 1, 1]. Imagine playing a game where one person picks one die, the other person picks one of the remaining dice, and the winner of the game is whoever rolls a higher number. Is there a winning die to pick?
If player 1 picks Die A, then player 2 would pick Die B, and have a ⅔ probability of winning (any time Die 2 shows a 6, it beats Die A’s 4). Likewise, if player 1 picked Die B, then player 2 would pick Die C, and have a 5/9 probability of winning (this comes from a ⅓ chance of a guaranteed win by rolling a 10, and a ⅔ chance of rolling a 1, times a ⅓ chance the other person rolled a 0). So is C the best die to pick? If player 1 started with that one, player 2 would pick Die A, and have a ⅔ probability of winning (any time player 1 rolled a 1). So in this case, B beats A, C beats B, and A beats C. This nontransitivity leads to more interesting game theory than strict ordering of outcomes. (This explains why Rock-Paper-Scissors is still played, despite its simple rule set.)
So how does this apply to fantasy football?
Imagine that you can field two different lineups. Lineup A has an expected point total of 97 points with a standard deviation of 5 points. Lineup B has an expected point total of 95 points with a standard deviation of 20 points. Which lineup should you play? It depends on your opponent.
If you were to play against yourself, Lineup A clearly does better; the difference between the two lineups is expected to be 2 points, with a standard deviation of 20.62 points.
This means Lineup A beats Lineup B 53.8% of the time (see Figure 1). This is clearly the stronger lineup.
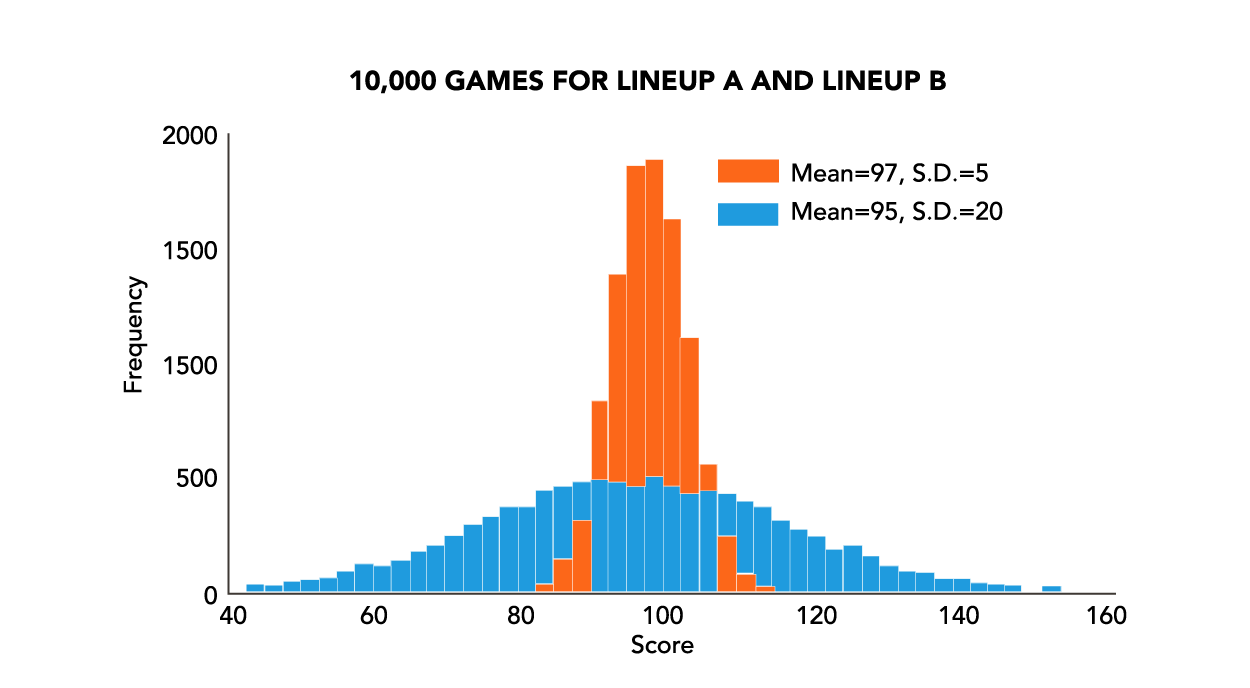
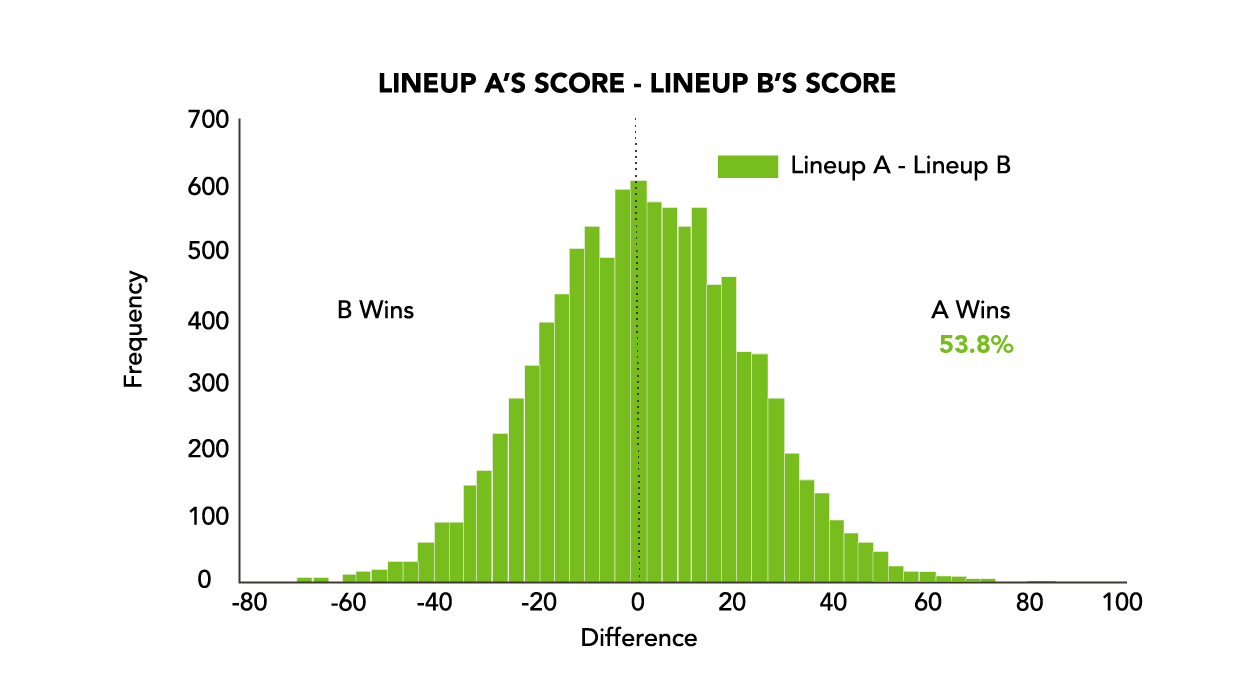
Figure 1: Lineup A wins 53.8% of the time versus Lineup B
What happens, though, if your opponent has a lineup with an expectation of 100 points and a standard deviation of 5 points? Your opponent is a favorite against either one of your lineups, but now, Lineup B is better to play than Lineup A! The additional variance in your point total increases your chance of winning. The expected loss if you play Lineup A is by 3 points with a standard deviation of 7.07 points, meaning you only win the game 33.6% of the time (see Figure 2).
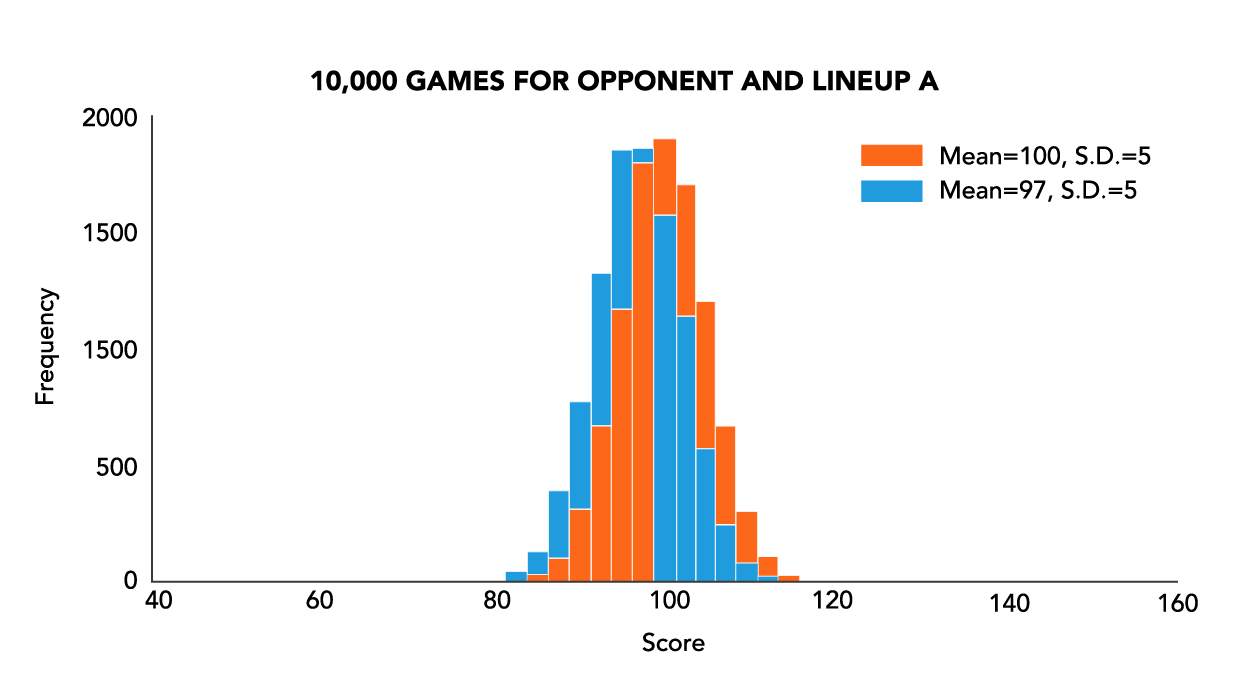
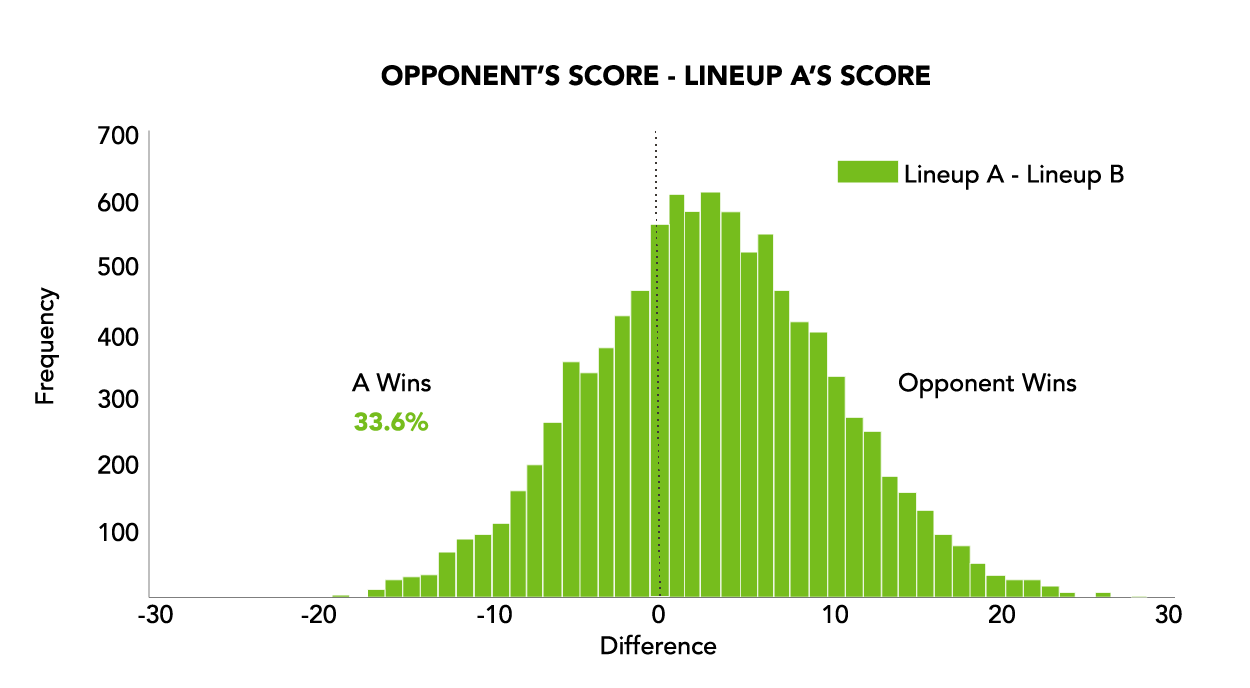
If you play Lineup B, though, you are still expected to lose (now by 5 points), but the standard deviation is 20.62 points, meaning you will end up winning the game 40.4% of the time (see Figure 3). In other words, if you were in this situation 100 times, you would expect to win an additional 7 games by having the “worse” team playing!
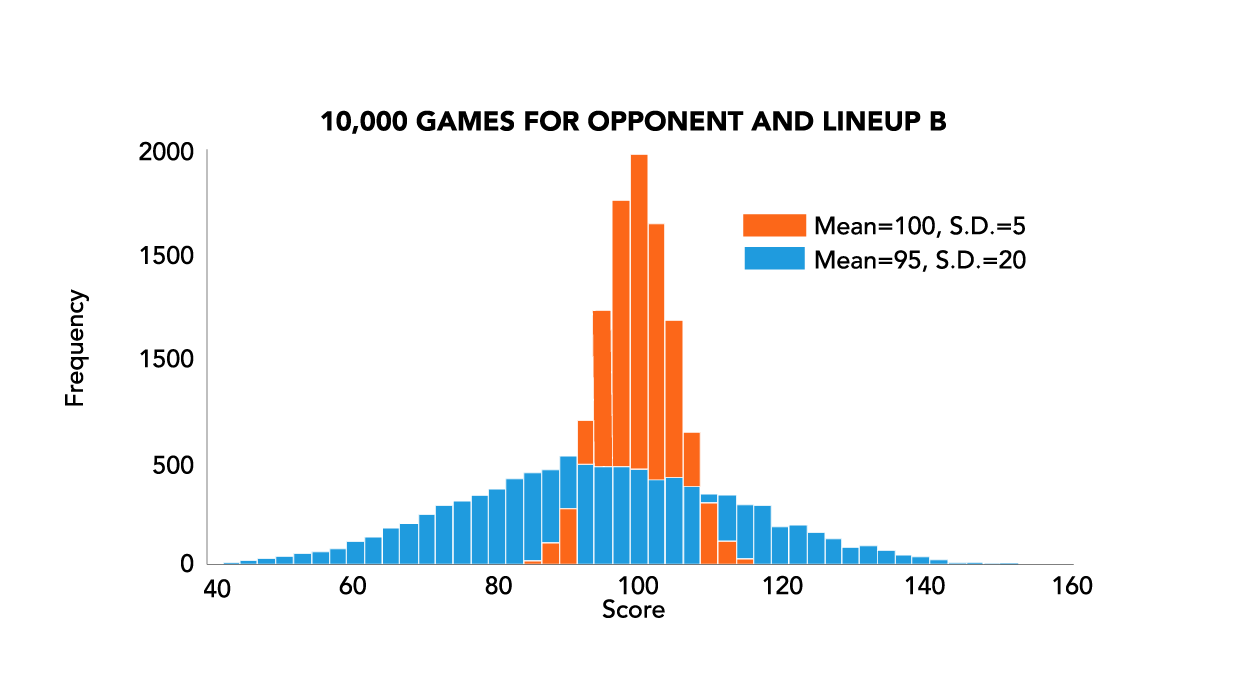
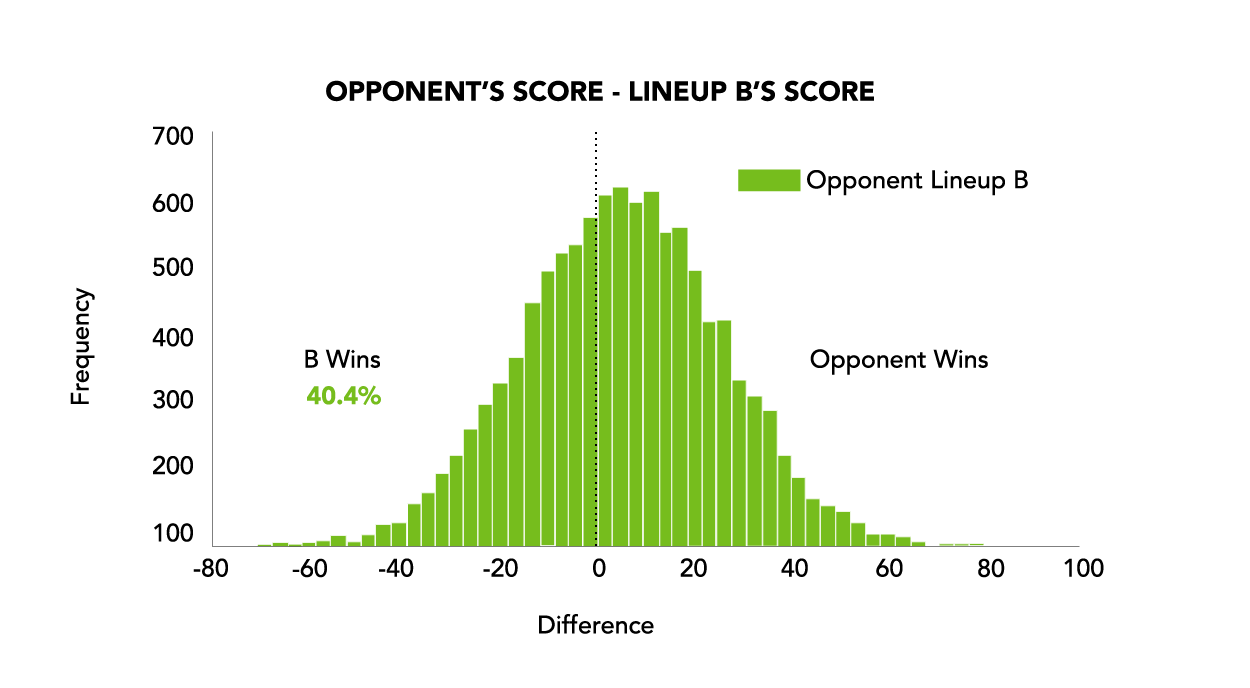
If you are the favorite in the game, though, you do not want to play your more volatile team. If we change the opponent’s expected point total to 92 instead of 100, then your Lineup A wins 58% of the time while Lineup B only wins 54% of the time.
To maximize your chances of winning your fantasy football league, you will need to take account of both expectation and standard deviation. In cases where you start your ‘worse’ lineup, fantasy sites like CBSSports and Yahoo may think you are a poor manager, but you can take comfort knowing you maximized your chances of winning your fantasy football matchup.
[SIDE NOTE ON THESE CALCULATIONS: For all of these calculations, I have made the simplifying assumption that scores are normally distributed (i.e., have a bell-shaped distribution). If you have two normal distributions X and Y, with respective means μX and μY and standard deviations σX and σY, then μ(X – Y) = μX – μY, and σ(X – Y) = √(σX2 + σY2). This assumes no correlation between the two distributions.]




Subscribe Now
Get each new post sent straight to your inbox